
The Heat Treat Doctor® has returned to offer sage advice to Heat Treat Today readers and to answer your questions about heat treating, brazing, sintering, and other types of thermal treatments as well as questions on metallurgy, equipment, and process-related issues.
This informative piece was first released in Heat Treat Today’s December 2024 Medical & Energy Heat Treat print edition.
The subject of thermal expansion and contraction is a very important one to most heat treaters given that the materials of construction of our furnaces and our fixtures experience these phenomena every day. However, to find a simple explanation of what it is and how we can help minimize the issues caused by it can be difficult. What we need is an explanation in laymen’s terms, along with some simple science and a few examples. Let’s learn more.
Thermal Expansion Effects

When exposed to a change in temperature, whether heating or cooling, materials experience a change (increase or decrease) in length, area, or volume. This not only changes the material’s size but also can influence its density. The freezing of ice cubes is a common example of a volume expansion (on freezing or cooling), while as they melt (on heating), we see a volume contraction.
As most of us recall from our science classes, as temperature increases, atoms begin to move faster and faster. In other words, their average kinetic energy increases. With the increase in thermal energy, the bonds between atoms vibrate faster and faster creating more distance between themselves. This relative expansion (aka strain) divided by the change in temperature is what is known as the material’s coefficient of linear thermal expansion.
We must also be aware, however, that a number of materials behave in a different way upon heating. Namely, they contract. This usually happens over a specific temperature range. Tempering of D2 tool steel is a good example (Figure 1). From a scientific point of view, we call this thermal contraction (aka negative thermal expansion).
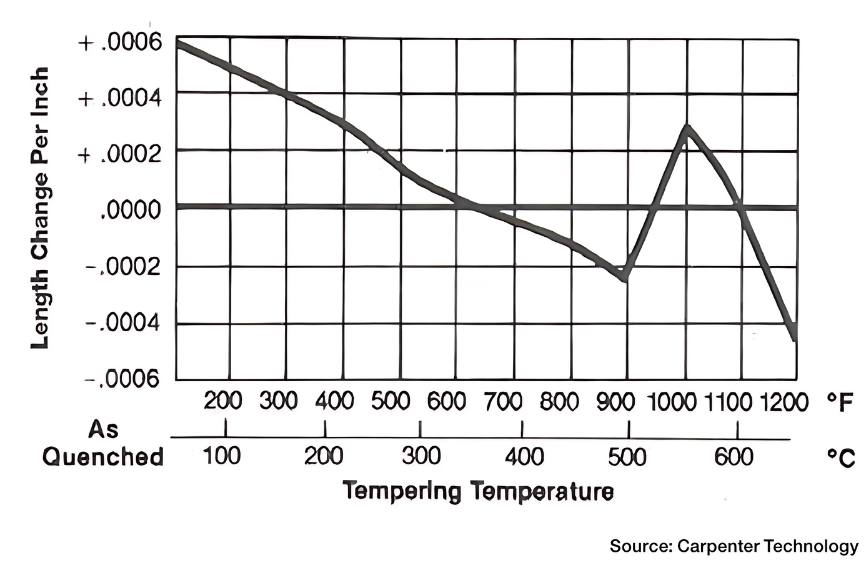
A related fact to be aware of is that thermal expansion generally decreases with increasing bond energy. This influences the melting point of solids, with higher melting point materials (such as the Ni-Cr alloys found in our furnaces and fixtures) more likely to have lower coefficient of thermal expansion. The thermal expansion of quartz and other types of glass (found in some vacuum furnaces) is, however, slightly higher. And, in general, liquids expand slightly more than solids.
Effect on Density
As addressed above, thermal expansion changes the space between atoms, which in turn changes the volume, while negligibly changing its mass and hence its density. (In an unrelated but interesting fact, wind and ocean currents are, to a degree, effected by thermal expansion and contraction of our oceans.)
What Is the Effect of the Coefficient of Thermal Expansion?
In laymen’s terms, the coefficient of thermal expansion (Table 1) tells us how the size of an object changes with a change in temperature. Specifically, it measures the fractional change in size per degree change in temperature at a constant pressure. Lower coefficients describe lower tendency to change in size. There are several types of thermal expansion coefficients — namely linear, area, and volumetric. For most solid materials, we are typically concerned in the heat treat industry with the change along a length, or in some cases a change in volume (though this is mainly of concern in liquids).

Heat Treat Furnace Examples
When calculating thermal expansion, it is necessary to consider whether the design is free to expand or is constrained. Alloy furnace muffles, retorts, mesh and cast link belts, and radiant tubes are good examples. The furnaces that use them must be designed to allow for linear growth and changes in area or volume. If not, the result is premature failure due to warpage (i.e., unanticipated movement).
If a component is constrained so that it cannot expand, then internal stress will result as the temperature changes. These stresses can be calculated by considering the strain that would occur if the design were free to expand and the stress required to reduce that strain to zero, through the stress/strain relationship (characterized by Young’s modulus). In most furnace materials it is not often necessary to consider the effect of pressure change, except perhaps in certain vacuum furnaces or autoclave designs.
A Little Science
For those that are interested, here are the formulas most often used by heat treaters to calculate the coefficient of thermal expansion.
Estimates of the Change in Length (L), Area (A), and Volume (V)
Linear expansion is best interpreted as a change in only one dimension, namely length. So linear expansion can be directly related to the coefficient of linear thermal expansion (αL) as the change in length per degree of temperature change. It can be estimated (for most of our purposes) as:

where:
- ΔL is the change in length
- ΔT is the change in temperature
- αL is the coefficient of linear expansion
This estimation works well as long as the linear expansion coefficient does not change much over the change in temperature and the fractional change in length is small (ΔL/L <<1). If not, then a differential equation (dL/dT) must be used.
By comparison, the area thermal expansion coefficient (αA) relates the change in a material’s area dimensions to a change in temperature by the following equation:
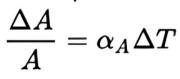
where:
- ΔA is the change in area
- ΔT is the change in temperature
- αA is the coefficient of area expansion
Again, this equation works well as long as the area expansion coefficient does not change much over the change in temperature ΔT(ΔT), if we ignore pressure and the fractional change in area is small (ΔA/A <<1)ΔA/A<<1. If either of these conditions does not hold, the equation must be integrated.
For a solid volume, we can again ignore the effects of pressure on the material, and the volumetric (or cubical) thermal expansion coefficient can be written as the rate of change of that volume with temperature, namely:
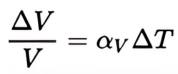
where:
• ΔV is the change in volume
• ΔT is the change in temperature
• αV is the coefficient of volumetric expansion
In other words, the volume of a material changes by some fixed fractional amount. For example, a steel block with a volume of 1 cubic meter might expand to 1.002 cubic meters when the temperature is raised by 90°F (32°C). This is an expansion of 0.2%. By contrast, if this block of steel had a volume of 2 cubic meters, then under the same conditions it would expand to 2.004 cubic meters, again an expansion of 0.2% for a change in temperature of 90°F (32°C).
Thermal Fatigue
In many instances, we must consider the effect of thermal fatigue as well as thermal stress. One example is on the surface of a hot work die steel as H11 or H13: one must ensure that in service, when it experiences a (rapid) change in temperature, it will avoid cracking.
The equation for thermal stress is:
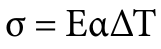
where:
- σ is the thermal stress
- E is the Young’s modulus of the material at temperature
- α is the coefficient of linear thermal expansion at temperature
- ΔT is the change in temperature
Here both E and α depend on temperature and the resultant stress will either be compressive if heated or tensile if cooled, so we must use these constants at both maximum and minimum temperatures. Considering the temperature dependent stress-strain curve, this stress may exceed the elastic limit (tensile or compressive) and contribute eventually to thermal fatigue failure. There are software programs to aid in the calculation of the resultant thermal stresses. Thermal expansion at a surface at a higher temperature than the core results in a compressive stress, and vice versa.
Final Thoughts
The effects of thermal expansion will be highlighted in a forthcoming article in Heat Treat Today, but it suffices for all heat treaters to remember that this phenomenon is responsible for a great deal of downtime and maintenance in our equipment. It also can affect the end product quality (disguising itself as distortion) and hence create additional cost or performance issues for our clients.
References
Chandler, Harry, ed. Heat Treater’s Guide: Practices and Procedures for Irons and Steels, 2nd Edition. ASM International, 1995.
Herring, Daniel H. Vacuum Heat Treatment. BNP Media, 2012.
Herring, Daniel H. Vacuum Heat Treatment Volume II. BNP Media, 2016.
Special thanks to Professor Joseph C. Benedyk for his input on the topic.
About the Author

“The Heat Treat Doctor”
The HERRING GROUP, Inc.
Dan Herring has been in the industry for over 50 years and has gained vast experience in fields that include materials science, engineering, metallurgy, new product research, and many other areas. He is the author of six books and over 700 technical articles.
For more information: Contact Dan at dherring@heat-treat-doctor.com.
For more information about Dan’s books: see his page at the Heat Treat Store.







